Hecho por:

MIGUEL ANGEL CELY ACUÑA   -  B192P

Detectores/generadores de parida

Generador de paridad . En los generadores de paridad la paridad puede ser par o impar. El bit de paridad se utiliza para detectar posibles errores en la transmisión del dato transmitido, mediante un comprobador de paridad que recepciona la información con el fin de validarla. Paridad par El bit de paridad será un 0 si el número total de 1 a transmitir es par.La suma de los bits que son unos, contando datos y bit de paridad dará siempre como resultado un número par de unos.

Resumen

Generadores de paridad Par/Impar Los circuitos electrónicos digitales se basan en la transmisión y el procesamiento de información, lo que hace necesario verificar que la información recibida es igual a la emitida; no suelen producirse errores, por lo que cuando ocurren en la mayoría de los casos el error en la transmisión se produce en un único bit. El método más sencillo y eficaz de comprobación de la transmisión de datos consiste en añadir a la información transmitida un bit más, con la misión de que el número de 1 transmitidos en total sea par (paridad par), o impar (paridad impar).

En los sistemas de transmisión y recepción de datos digitales es necesario comprobar errores en la información enviada. Esto se realiza chequeando los bits que forman el dato de manera tal que el receptor pueda detectar y/o corregir si hubo cambio en uno o más bits. Se realiza de la misma manera que el de paridad par pero con la condición de que el bit de paridad P se complete con 1 si es par y 0 si es impar ya que el diseño es para un generador de paridad impar.

Los generadores de paridad par son aquellos circuitos que generan un 0 cuando el número de 1 en la entrada es par y un 1 cuando es impar, en el caso de dos bit, sería como se muestra en la tabla de verdad: P = paridad par, es decir un número de 1 par. I = paridad impar, es decir un número de 1 impar. Las funciones canónicas serán

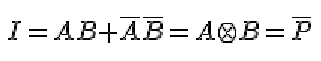
Cuya posible implementación se muestra en la figura:

Paridad par: El bit de paridad será un 0 si el número total de 1 a transmitir es par. La suma de los bits que son unos, contando datos y bit de paridad dará siempre como resultado un número par de unos.

Paridad impar: El bit de paridad será un 1 si el número total de 1 es impar, el número de unos (datos + paridad) siempre debe ser impar. Se realiza con la misma manera que el de paridad par pero con la condición de que el bit de paridad P se complete con 1 si es par y 0 si es impar ya que el diseño es para un generador de paridad impar. 

Ejemplos

Tenemos el dato original 0111001. Vemos que la trama a transmitir tiene un número par de unos (4). Al añadir el bit de paridad obtendremos el siguiente carácter, que es el que se transmitirá a destino: 1.   Si usamos paridad par, ya hay un número par de unos, por tanto se añade un 0, y transmitiremos 00111001. 2.   Si usamos paridad impar, como hay un número par de unos, hemos de añadir otro 1 para conseguir un número impar, y transmitiremos 10111001 Aplicación Los generadores de paridad se usan en Telecomunicaciones para detectar, y en algunos casos corregir errores en la transmisión de datos.  

DETECTOR DE PARIDAD: Los circuitos electrónicos digitales están basados en la transmisión y el procesamiento digital de la información, lo que hace necesario verificar que la información, lo que hace necesario verificar que la información recibida es igual a la transmitida, para esto es necesario realizar una detección de error. Detector de Paridad Par

Detector de Paridad Impar

Método de paridad para la detección y corrección de errores: Códigos de Hamming Además de los bits de paridad, existen otros códigos específicos que también permiten realizar la detección de errores. Uno de estos es el código Hammning mediante el cual se puede detectar un error y corregirlo. El código Hamming extendido permite detectar dos errores. En el código Hammnig se emplean varios bits de paridad (BP) en lugar de un único bit para todo el paquete de datos (o palabra) a enviar. Cada uno de los bits de paridad se genera a partir de un grupo de bits (un subgrupo) de la palabra (palabra: D0, D1, D2,...Dn-1)) de datos. Por ello, el primer paso será decidir el número de bits de paridad que habrá que añadir. Este número debe cumplir la siguiente inecuación: 2k ³ n + k + 1 Þ Bp1, Bp2,…Bpk (Bits de paridad) Donde k es el número de bits de paridad a añadir a la palabra de n bits. Por lo tanto, la palabra nueva tendrá k + n bits, y cada k bit es un bit de paridad de un subgrupo de bits de la palabra a transmitir. Cada bit de paridad debe ocupar una posición concreta en la nueva palabra a transmitir. Esa posición se define utilizando la expresión: PBpi = 2i-1 (i=1,..k) Þ posición del bip de paridad i-ésimo

El segundo paso será definir los grupos de bits (o sub grupos) a partir de la nueva palabra de datos, es decir la compuesta por los bits de información y los bits de paridad. También habrá que asignar a cada sub grupo uno de los bits de paridad creados Bpk (i=1,..k). Para ello, habrá que generar una lista de números desde 0 hasta (2k-1). A continuación, esos números se deben expresar en binario natural. Teniendo en cuanto ese formato, se analiza el valor de cada uno de los bits de todos los números de la lista, es decir, los bits de la posición 20, los de la posición 21 y los de la posición 22. En cada caso, se anota el número que contiene un 1. Los números obtenidos así indican la posición de los bits que formarán cada sub grupo. Un ejemplo de aplicación se muestra en la siguiente figura para un paquete de información de 4 bits, es decir, n = 4.

Se observa que cada sub grupos incluye la posición correspondiente aun bit de paridad, lo cual no tiene ningún sentido, ya que, estos grupos son precisamente para generar los bits de paridad. Por ello, habrá que eliminar de cada sub grupo ese bit y ese grupo será el que genere el bit de paridad que ha habido que eliminar.

Fuentes

• Microelectronics, Jacob Millman, 1979
• Electrónica Digital. Julio Díaz Calvo. Editorial Pueblo y Educación, 1989
• Circuitos Electrónicos Digitales.Elías Muñoz Merino. Editorial Pueblo y Educación, 1990